
Biegeschwingungen von Papierrollen
Ein Beitrag zu einem aktuellen Problem bei überbreiten Tiefdruck- und Zeitungsdruckmaschinen
Prof. Dr. Karl Haller
Die Ursprünge dieser Abhandlung gehen auf die Vorlesung "Rollendruckmaschinen" zurück, die Autor bei seiner Lehrtätigkeit im Studiengang Druck- ud Medientechnik der Fachhochschule München gehalten hat.
1. Problembeschreibung
Biegeschwingungen von ablaufenden Papierrollen sind vor allem bei überbreiten und schnellen Tiefdruck- und Zeitungsdruckmaschinen zu beachten, da Resonanzgefahr besteht.Die Leistungsspitze liegt derzeit
- im Tiefdruck bei 4,32 m Rollenbreite, ca. 16 m/s Bahngeschwindigkeit und unter Verwendung von Hartpapierhülsen mit 150 mm Innendurchmesser,
- im 6-Seiten-breiten Zeitungsdruck bei bis zu 2,5 m Rollenbreite, ca. 15 m/s Bahngeschwindigkeit und unter Verwendung von Hartpapierhülsen mit 76 mm Innendurchmesser.
Die Brutto-Produktion einer Rollendruckmaschine ist immer das Produkt von maximaler Bahnbreite und maximaler Bahngeschwindigkeit. Dies gilt für alle Druckverfahren und ist unabhängig von den Durchmessern der Form- oder Plattenzylinder. Hinter der Forderung nach höherer Produktivität steckt nicht nur der Wettbewerk im Druckmarkt, sondern auch der Wettbewerb mit den elektronischen Medien, deren Aktualitätsvorsprung den Zeitungs- und Zeitschriftenbereich zu weiteren Leistungssteigerungen anspornt.
Es ist derzeit von keinem Druckverfahren eine physikalische Obergrenze für die Druckgeschwindigkeit bekannt. Im Tiefdruck sind bereits Tests mit 23 m/s Bahngeschwindigkeit gefahren worden, allerdings durch nicht praxisgerechte Umgehung der hier anstehenden Problematik.
Sicherlich stellt der Falzapparat die derzeitige mechanische Grenze für weitere Geschwindigkeitssteigerungen dar. Von der European Rotogravure Association (ERA) stammt der Vorschlag, die (historische) online-Koppelung des Falzapparates an die Druckmaschine aufzugeben. Statt dessen soll von Rolle auf Rolle gedruckt werden, wobei aber die Papierbahn vor dem Aufrollen in die einzelnen Stränge aufgeschnitten werden soll. Das Falzen soll offline mit mehreren parallel und von der Druckmaschine unabhängig laufenden Falzmaschinen erfolgen. Damit wäre der Weg frei zu weiteren Geschwindigkeitssteigerungen der Druckmaschine. Kostenrechnungen haben offensichtlich nicht das gewünschte Ergebnis gezeigt.
Die Entwicklung der Druckgeschwindigkeiten über die letzten Jahrzehnte zeigt, dass man eher von einer Sättigung als von einer Stagnation sprechen sollte. Die Produktionssicherheit lässt auch mit steigender Druckgeschwindigkeit nach. Somit ist es nicht erstaunlich, dass die gewünschte Erhöhung der Produktivität nicht in der Bahngeschwindigkeit, sondern in der Bahnbreite gesucht wird.
Die Papierindustrie beweist zwar, dass Bahngeschwindigkeiten bis 30 m/s beherrschbar sind und das bei Bahnbreiten von über 9 m! Warum nicht auch in der Druckmaschine bei Eliminierung des Falzapparates (und eventuell auch der bremsenden Wendestangen)? Der entscheidende Unterschied besteht darin, dass die Papierrolle auf den Umrollstationen gänzlich anders gelagert ist als in der Druckmaschine. Bei den Umrollern unterscheidet man zwischen der Tragwalzenumrollern und der Stützwalzenumrollern. Beiden ist gemeinsam, dass die aufzuwickelnde Papierrolle über die gesamte Breite auf den beiden Tragwalzen bzw. der zentralen Stützwalze aufliegt. Bei der Druckmaschine sind diese Lagerungsarten nicht einsetzbar; bei allen Rollendruckmaschinen wird die Papierrolle in der Achse gelagert. Von Ausnahmen abgesehen, wird aber keine durchgehende (Stahl-) Achse benutzt, sondern kurze Achszapfen mit radialen Spreizbacken, auch Pinolen genannt, die nur bei schmalen Maschinen weniger als 100 mm, bei breiten Maschinen maximal 300 mm in die Hülse der Papierrollen hineinreichen. Diese Lagerungsart ist unabdingbar für einen automatischen Rollenwechsel bei voller Produktion. Die früher üblichen Konen, die die Rolle durch axiale Anpressung gehalten haben, sind nur noch bei Alt-Maschinen anzutreffen. Sie wären für den hier genannten Hochleistungsbereich gänzlich ungeeignet.
Es liegt bei den "Jumbo-" Rollen des Tiefdrucks folgende Situation vor: Die Papierrolle ist ca. 4,4 m breit und wird links und rechts nur in zwei Zapfen (Spanndorne, Pinolen) gelagert, die 300 mm (Eintauchtiefe) in die Hülse hineinragen.
Bei den 6-Seiten-Zeitungsdruckmaschinen beträgt die Rollenbreite bis zu 2500 mm und die Pinoleneintauchtiefe nur etwa 100 mm.
Bekanntlich sind alle mechanischen Systeme schwingungsfähig; bei der Papierrollenlagerung in der Druckmaschine liegen besonders ungünstige Verhältnisse vor. Mit einigem mathematischen Aufwand kann man zeigen, dass in bestimmten Situationen beim Verdrucken der Papierrolle eine Resonanzfrequenzen der Rolle durchfahren werden müssen. Im Resonanzfall können sich die Schwingungen bis zum Bruch der Rolle aufschaukeln.
Aus einer 1998 erschienenen Firmenschrift eines einschlägigen Druckmaschinenherstelles kann man entnehmen, dass bei der Lagerung der Papierrolle im Rollenwechsler keine grundsätzliche neue konstruktive Lösung in Sicht ist.
Zur Verbesserung der Situation haben die Hülsenhersteller ihre Produkte im letzten Zeitraum wesentlich verbessert. Die Steigerung des Elastizitätsmoduls (E-Modul) stand dabei im Vordergrund der Bemühungen, die Eigenfrequenz der Hülsen anzuheben. Vielfach muss dabei auch eine Erhöhung der Dichte in Kauf genommen werden, was den Erfolg durch die Steigerung des E-Moduld wieder etwas herabsetzte.
Wie später gezeigt wird, sind wesentlich stärkere Verbesserungen zu erwarten, wenn der Innendurchmesser der Hülse erhöht wird, was bei oberflächlicher Betrachtung nicht sofort einsehbar ist.
Die Rollenhülse besteht aus spiralförmig aufgewickelten und verklebten Hartpapierstreifen. Forderungen nach einer Hülse aus Aluminium, Stahl oder faserverstärkten Kunststoffen werden immer wieder erhoben; eine genauere Diskussion ergibt, dass diese Forderung für die breite Anwendung (noch) nicht realistisch ist und möglicherweise wegen der aus Kostengründen notwendigen Wiederverwendung und der damit verbundenen Beschädigungs- und Verformungsgefahr letzlich sogar die Situation verschlechtern könnte. Immerhin ist festzuhalten, dass im Jahre 2006 erste Anwendungen mit Aluminiumhülsen bekannt wurden, zuerst im überbreiten Zeitungsdruck mit sechs Seiten in der Breite, später aber auch im Tiefdruck. Die Praxiserfahrungen sind abzuwarten.
In der DIN 6748 (Ausgabe Mai 1984) sind die Innendurchmesser der Hartpapierhülsen in folgenden Größen festgelegt:
- 70 mm
- 76 mm, 76er Hülse, Vorzugsgröße (3-Zoll-Hülse, 3" = 76,2 mm)
- 100 mm
- 120 mm
- 150 mm, 150er Hülse, Vorzugsgröße (6-Zoll-Hülse, 6" = 152,4 mm)
- 200 mm, 200er Hülse
- 250 mm
- 300 mm, Vorzugsgröße
Der Außendurchmesser bzw. die Hülsenwanddicke sind in der Norm nicht festgelegt, sondern sind zwischen Hersteller und Abnehmer zu vereinbaren. Typische Werte für Hülsenwanddicke sind 15 mm für Hülsen mit 76 mm Innendurchmesser und 13 mm für Hülsen mit 150 mm Innenduchmesser. Bei der Übeschreitung der 4-m-Grenze im Tiefdruck werden aber auch 150er Hülsen mit 15 mm Wanddicke geliefert. Mit diesen Daten erhält man für die 76er Hülse einen Außendurchmesse von 106 mm, für die 150er Hülse einen Außendurchmesser von 176 mm oder 180 mm. Der Außendurchmesser der Rollenhülse bzw. die Hülsenwanddicke ist für die Eigenfrequenz nicht sehr von Belang, wohl aber für die Festigkeit.
Bei breiten Tiefdruckmaschinen wird die Papierrolle über umlaufende Gurte angetrieben bzw. gebremst, in allen anderen Fällen über das Zentrum. Bei Zentrumsantrieb muss das gesamte Drehmoment über die Hülse geleitet werden, was in günstigen Fällen wie beim kurzzeitigen Vorrücken der vollen Rolle beim Einrichten der Maschine oder beim Not-Stopp zu erheblichen Torsionsbelastung der Hülse führt. Bei Gurtantrieb muss die Rolle gegen Ende aus den Gurten herausgeschwenkt werden. Es fehlt dann die stützende Wirkung der Gurte. Für die Bremsung bzw. Antrieb sorgt dann ein klein dimensionierter Zentrumsantrieb.
2. Die maßgebenden Geometrie- und Stoffdaten einer Hülse bzw. Papierrolle
Die folgende Abbildung veranschaulicht die maßgebenden Abmessungen und Stoffdaten der Hülse und der Restrolle. Der Ausgangsdurchmesser der Papierrolle D beträgt üblicherweise 1250 mm oder 1270 mm (50" = 1270 mm). In zunehmenden Maße werden Papierrollen mit 1500 mm oder 1524 mm Durchmesser eingesetzt (60" = 1524 mm).
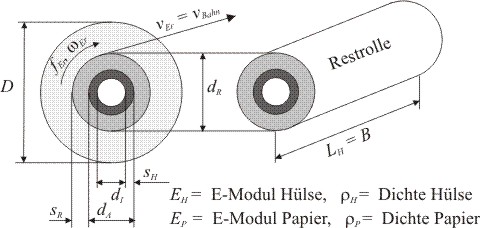
Abbildung 1: Die Geometrie- und Stoffdaten der Restrolle und der Hülse
Schwingungskritische Situationen treten erst dann ein, wenn die Rolle ihrem Ende entgegengeht, in üblichen Situationen bei Restlagendicken sR im Allgemeinen unter 30 mm. Oft sind erst die letzten 10 mm kritisch. Die Natur ist doch so freundlich, dass Resonanzen nicht schon bei großen Restrollendurchmessern dR entstehen.
In der späteren Ableitung treten mit dem Querschnitt A und dem Flächenmoment zweiten Grades I vorübergehend weitere Geometriedaten auf, die aber für die Arbeitsformeln auf die genannten Durchmesser zurückgeführt werden.
Die maßgebenden Stoffdaten sind
- der Elastizitätsmodul (E-Modul), Formelzeichen E, Einheit z. B. in N/mm2 oder N/m2 und
- die Dichte, Formelzeichen ρ, Einheit z. B. in kg/m3
Für die Einheit des E-Moduls wird mitunter auch "MPa" (Mega-Pascal) benutzt. Das ist formal zulässig, da 1 MPa = 1 N/mm2 . Somit sind die Zahlenwerte gleich. Dennoch sollte man die Einheit MPa nicht benutzen, da sonst unnötig Verwirrung entstehen könnte. In der Hülsennorm DIN ISO 11093-8 wird auch die Einheit N/mm2 für den E-Modul benutzt.
Die E-Moduln der Hartpapierhülsen liegen zwischen 3500 und 7000 N/mm2, bei Dichten zwischen 750 und 1000 kg/m3. Konkret zutreffende Werte sind den Spezifikationen der Hülsenhersteller zu entnehmen.Beim Papier ist nur die Dichteangabe zweifelsfrei. Sie liegt über alle Rollenpapiersorten betrachtet zwischen 900 und 1400 kg/m3.
In der Literatur findet man im Zusammenhang mit Papierrollenschwingungen höchst unterschiedliche Angaben für den E-Modul von Papier. Die Werteskala reicht von 1000 bis 6000 N/mm2. Es ist bekannt, dass der E-Modul eines Papiers in Querrichtung gemessen wegen der Papiervorzugsrichtung um den Faktor 3 bis 5 kleiner ist als in Längsrichtung. Betrachtet man die Papierrolle als Biegebalken, bei dem die untere Faser bei Belastung gedehnt und die obere Faser gestaucht wird, dann erkennt man, dass für die Schwingungsbetrachtung in erster Linie der (leider kleinere) E-Modul des Papiers in Querrichtung maßgebend ist; eventuell spielt auch der E-Modul in Dickenrichtung eine kleine Rolle, genauer der Schubmodul, der aber mit dem E-Modul über die Querkontraktionsziffer des Papiers zusammenhängt. Übliche E-Modul-Messungen werden statisch an planen Einzelpapierproben durchgeführt. In der Restrolle sind aber die einzelnen Papierlagen unter einer (unbekannten) Wickelspannung aufgewickelt und werden ausgesprochen dynamisch belastet. Nach dem jetzigen Wissensstand kann der schwingungsrelevante E-Modul nur durch Schwingungsmessungen ermittelt werden, die zwar nicht schwierig, aber doch etwas aufwändig sind. Für den so ermittelten E-Modul ist auch die Bezeichnung "E-Modul des Papierzylinders" gebräuchlich; es gibt aber auch noch andere Bezeichnungen. Nach bisherigen Messungen hängt der schwingungsrelevante E-Modul des Papiers auch von der Restlagendicke sR ab, was die Sache noch weiter kompliziert. Im Einzelfall können konkrete Werte zur Zeit nur von den Hülsenherstellern oder Papierherstellern in Erfahrung gebracht werden. In der Literaturstelle [5] sind aber Orientierungswerte zu finden.
3. Die Differenzialgleichung eines Balkens
Für die Ableitung der Schwingungsdifferenzialgleichung muss die Papierrolle zu einem beidseitig fest gelagerten Balken abstrahiert werden:
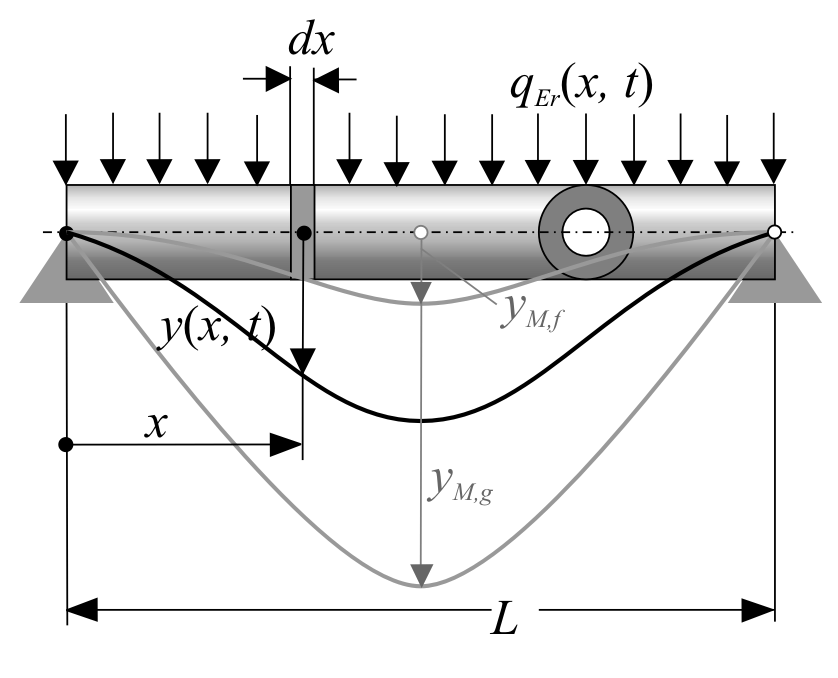
Abbildung 2: Die Papierrolle als schwingender Balken
Aus der Theorie der Balkenbiegung sind Biegemoment M und Querkraft Q wie folgt bekannt:
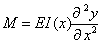
Darin ist E der Elastizitätsmodul der Papierrolle und I das (axiale)
Flächenmoment zweiten Grades der Kreisring-Querschnitts.
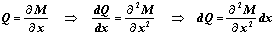
oder:
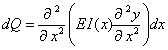
Das dynamische Kräftegleichgewicht fordert:
Trägheitskraft + Rückstellkraft = Erregerkraft
und muss nun für die differenziell kleine Scheibe der Papierrolle mit der Breite dx aufgestellt werden.
Die Trägheitskraft ist gegegeben durch das Produkt dm*a Darin ist dm die differentiell kleine Masse
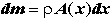
mit der Dichte ρ und dem Querschnitt A.
Die Beschleunigung a in y-Richtung ist gegeben mit:
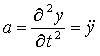
Die Rückstellkraft ist durch die differenziell kleine Querkraft dQ gegeben, die Erregerkraft durch das Produkt qEr(x,t)dx. Somit kann man das Kräftegleichgewicht wie folgt angeben:
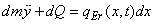
Man beachte die Analogie zum Kräftegleichgewicht eines schwingenden Feder/Masse-Systems:
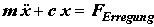
Der wesentliche Unterschied besteht nur darin, dass die (starre) Masse m des Feder/Masse-Systems durch die differentiell kleine Masse dm und die Federkraft durch die differentiell kleine Querkraft dQ ersetzt werden müssen.
| (1) | 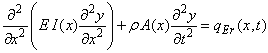 |
Für Kreisringquerschnitte mit Außendurchmesser D und Innendurchmesser d gilt allgemein:
| (2) | 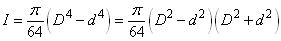 |
| (3) | 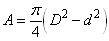 |
Für die Restrolle gilt: D = dR, d = dA Eine wesentliche Besonderheit gegenüber der Schwingung eines Balkens besteht bei der Rolle darin, dass sich das Flächenmoment zweiten Grades und auch der Querschnitt durch den abnehmenden Durchmesser laufend verändern. Damit ändert sich letztlich auch laufend die Eigenfrequenz. Diese Merkmale liegen bei einem schwingenden Balken mit gleichbleibendem Querschnitt nicht vor.
Wenn man sich vorrangig für die Eigenfrequenzen interessiert, kann die auf der rechten Seite stehende Störgröße qEr(x, t) zu Null gesetzt werden. Der Ansatz (1) berücksichtig keine Dämpfung, das ist zwar nicht praxisgerecht, da Dämpfungen durch das Papier aufgrund seiner visko-elastischen Eigenschaften vorliegen. Dämpfend wirken neben dem Papierzug auch die Antriebsgurte, egal sie von oben oder – wie bei neueren Konstruktionen zur Lagerentlastung und Reduzierung der Rollendurchbiegung - unten angeordnet sind. Dabei ist noch zu bedenken, dass gerade in der kritischen Phase vor dem Rollenwechsel die (kleine) Rolle aus den Antriebsgurten herausgefahren werden muss, die Gurtdämpfung also nicht mehr wirken kann. Resonanzfrequenzen treten gerade bei kleinen Rollendurchmessern auf.
Die quantitative Erfassung der Dämpfung ist schwierig. Nun ist aber bekannt, dass die Dämpfung zwar für die Größe der Schwingungsamplituden bestimmend ist, aber nur geringen Einfluß hat auf die Frequenz, bei der die maximalen Schwingungsamplituden auftreten. In der nachfolgenden Betrachtung stehen die Resonanzfrequenzen im Mittelpunkt des Interesses, so dass es vertretbar ist, die Dämpfung zu vernachlässigen.
4. Die Lösung der Differenzialgleichung
Selbst mit den genannten Einschränkungen ist die Lösung der Differenzialgleichung mit einigem mathematischen Aufwand verbunden. Auf die Darstellung der Einzelschritte wird an dieser Stelle verzichtet; sie sind in der früher erwähnten Ausarbeitung enthalten.Die Lösung "Schwingweg y als Funktion von der Strecke x und der Zeit t" stellt sich wie folgt dar:
| (4) | 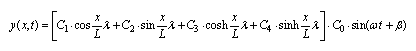 |
Die Größen C0, C1, C2, C3, C4 und β sind Integrationskonstanten, die aus den Rand- und Anfangsbedingungen bestimmt werden müssen.
Mit ω ist die noch unbekannte Eigenkreisfrequenz bezeichnet.
Die Größe λ (Lambda) ist zunächst eine Abkürzung gemäß:
| (5.1) | 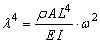 |
- ρ die Dichte der Rolle
- L die Rollenbreite
- E den Elastizitätsmodul
- A den vom aktuellen Rollendurchmesser abhängigen Querschnitt der Rolle
- I das vom aktuellen Rollendurchmesser abhängige Flächenmoment zweiten Grades der Rolle.
- ω die Eigenkreisfrequenz
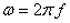
erhält man:
| (5.2) | 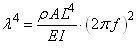 |
| (5.3) | 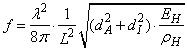 |
| (6.1) | 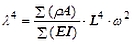 |
| (6.2) | 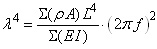 |
| (6.3) | 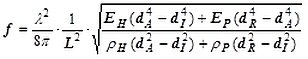 |
5. Die Lagerung der Hülse bzw. Restrolle. Die Eigenwerte λ
Für die weitere Vorgehensweise muss man sich Gedanken über die Art der Lagerung (Einspannung) der Rolle machen. In der Theorie der Balkenbiegung und -schwingung unterscheidet man bezüglich der Einspannung sechs Fälle; sie sind in der folgenden Abbildung schematisch dargestellt:
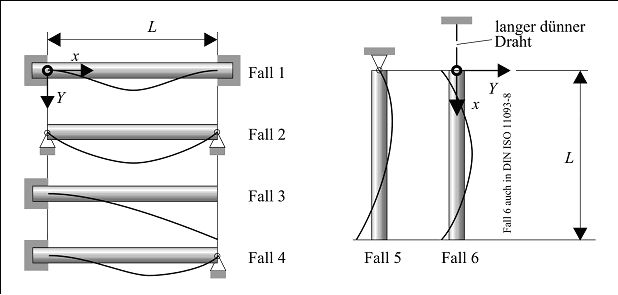
Abbildung 3: Die sechs Lagerungsfälle des Balkens
Von den beiden eher theoretisch erscheinenden Fällen 5 und 6 ist der Fall 6 bemerkenswert. Er stellt die "beidseitig freie" Einspannung dar, die streng genommen nur im Zustand der Schwerelosigkeit realisiert werden kann. Durch eine senkrechte Aufhängung an einem Draht kann der Balken in horizontaler Richtung als "beidseitig frei" betrachtet werden. Es kann gezeigt werden, dass der Fall 6 trotz gänzlich anderer Schwingungsformen zu den gleichen Lambda-Eigenwerten λ und somit auch zu gleichen Eigenfrequenzen wie im Fall 1 führt. Von diesem sehr bemerkenswerten Umstand wird in der Hülsennorm DIN ISO 11093-8 "Bestimmung der Eigenfrequenz und des Elastizitätsmoduls durch experimentelle Schwingungsanalyse" Gebrauch gemacht.
In der folgenden Tabelle stehen in den Zeilen 2 und 3 die Randbedingungen für alle sechs Einspannungsarten. Dabei steht Y abkürzend für y = f(x), also für die Schwingungsform. Y' steht dann für die erste Ableitung, Y'' für die zweite Ableitung und Y''' für die dritte Ableitung der Schwingungsform. Nebenbei: Man kann zeigen, dass die Schwingungsform qualitativ nur minimal von der Biegeline der statischen Balkenbiegung abweicht.
| 1 | Fall 1 | Fall 2 | Fall 3 | Fall 4 | Fall 5 | Fall 6 | |
| 2 | x = 0 | Y = 0 Y' = 0 |
Y = 0 Y'' = 0 |
Y = 0 Y' = 0 |
Y = 0 Y´= 0 |
Y = 0 Y'' = 0 |
Y'' = 0 Y''' = 0 |
| 3 | x = L | Y = 0 Y' = 0 |
Y = 0 Y'' = 0 |
Y'' = 0 Y'''= 0 |
Y = 0 Y''= 0 |
Y'' = 0 Y''' = 0 |
Y'' = 0 Y''' = 0 |
| 4 | Eigenwert- gleichung |
cosλ * coshλ - 1 = 0 |
sinλ = 0 | cosλ * coshλ + 1 = 0 |
tanλ - tanhλ = 0 |
tanλ - tanhλ = 0 |
cosλ * coshλ - 1 = 0 |
| 5 | 1. Eigenwert | λ1 = 4,730041 ≈ 4,730 |
λ1 = 3,141793 ≈ 3,142 |
λ1 = 1,875104 ≈ 1,875 |
λ1 = 3,926602 ≈ 3,927 |
λ1 = 3,926602 ≈ 3,927 |
λ1 = 4,730041 ≈ 4,730 |
| 6 | 2. Eigenwert | λ2 ≈ 7,853 | λ2 ≈ 6,283 | λ2 ≈ 4,694 | λ2 ≈ 7,069 | λ2 ≈ 7,069 | λ2 ≈ 7,853 |
| 7 | 3. Eigenwert | λ3 ≈ 10,996 | λ3 ≈ 9,424 | λ3 ≈ 7,855 | λ3 ≈ 10,210 | λ3 ≈ 10,210 | λ3 ≈ 10,996 |
In den bisher bekannten Ausarbeitungen über die Schwingungen der Papierrolle geht man davon aus, dass die Rolle "beidseitig fest gelagert" ist, entsprechend dem Fall 1 in der Abbildung. Ob dieser Fall bei 3,6 m Rollenbreite und 150 mm Pinoleneintauchtiefe wirklich vorliegt, kann durchaus in Frage gestellt werden.
Die Ergebnisse der Berechnungen fallen merklich anders und auch kritischer aus, wenn man den Fall 2 mit "beidseitig gelenkig gelagert" annimmt.
Die Praxis liegt zwischen den beiden Grenzfällen. Mit dem empirisch zu bestimmenden Einspannfaktor wird ausgehend vom Idealfall "beidseitig fest" eine Korrekturgröße eingeführt. Die Fälle 3 "einseitig (fest) gelagert", 4 "einseitig fest, einseitig gelenkig gelagert" und 5 "einseitig gelenkig gelagert, einseitig frei" sind für das Papierrollenproblem nicht relevant, können aber mit den gleichen mathematischen Werkzeugen behandelt werden.
Wenn man die in den Zeilen 2 und 3 aufgeführten Randbedingungen in die Lösung der Schwingungsdifferenzialgleichung einsetzt, erhält man zunächst ein homogenes lineares Gleichungssystem mit vier Gleichungen für die Bestimmung der vier Integationskonstanten C1, C2, C3 und C4. Nach einigen Umformungen verbleibt ein homogenes lineares Gleichungssystem mit zwei Gleichungen und zwei unbekannten Integrationskonstanten. Bekanntlich hat ein homogens lineares Gleichungssystem nur dann eine nichttriviale Lösung, wenn die Determinate des Gleichungssystems zu Null wird. Mit dieser Bedingung erhält man die charakteristischen "Eigenwertgleichungen", in der Zeile 4 der Tabelle aufgeführt sind. Diese Eigenwertgleichungen enthalten trigonometrische und mit Ausnahme von Fall 2 auch noch hyperbolischen Funktionen. Als Argument enthalten diese Funktionen nur noch den "Eigenwert" λ (Lambda), mit denen später die Eigenfrequenzen berechnet werden.
Im Fall 2 kann man unmittelbar erkennen, dass die Eigenwertgleichung unendlich viele diskrete Lösungen besitzt: λi = i * π, mit π = Kreiszahl 3,141595, i = 1, 2, 3, ...
In den anderen Fällen sind die Eigenwertgleichungen tranzendent und werden zweckmäßigerweise mit einem iterativ arbeitenden Computerprogramm berechnet. Auch in diesen Fällen zeigt sich, dass die Eigenwertgleichungen unendlich viele diskrete Lösungen besitzen, typisch für ein Kontinuum, das Feder und Masse in einem Bauteil vereint. Für alle sechs Fälle sind die drei ersten Eigenwerte in der Tabellen 5 bis 7 angegeben.
Mit dem ersten Eigenwert λ1 wird nach (5.3) buw. (6.3) die Eigenfrequenz der Resonanz erster Ordnung berechnet, mit λ2 die der Resonanz zweiter Ordnung berechnet usw.
In der Regel, und die trifft für Papierrollen immer zu, ist die Resonanz erster Ordnung am gefährlichsten. Deshalb bezeichent man die Eigenfrequenz f1 für die Resonanz erster Ordung mit kritische Frequenz und die damit berechnete Umfangsgeschwindigkeit vkrit der Rolle oder Hülse mit kritische Geschwindigkeit.Zur Erregerfrequenz Die gefährliche Resonanz liegt vor, wenn Eigenfrequenz und Erregerfrequenz übereinstimmen. Man kann aus (6.3) erkennen, dass sich die Eigenfrequenz in Abhängigkeit von Durchmesser dR der Restrolle ständig ändert. Aber auch die Erregerfreqzenz ändert sich bei gleichbleibender Bahngeschwindigkeit mit abnehmenden Rollendurchmesser ständig.
Die Erregerfrequenz kann man einfach angeben mit:
| (7) | 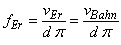 |
Für das Restrolle gilt: d = dR Im Resonanzfall stimmen die aus der Drehzahl der Rolle resultierende Erregerfrequenz mit der Eigenfrequenz der Rolle überein und die Schwingungsamplituden wachsen theoretisch über alle Grenzen. Da praktisch immer eine gewisse Dämpfung vorliegt, bleiben die Schwingungsamplituden endlich, können aber so große Werte annehmen, dass ein Bruch erfolgt. Dabei können Mitarbeiter zu Schaden kommen oder Anlagenteile beschädigt werden. Auf jeden Fall ist ein Bruch mit einer Produktionsstörung und mit Kosten verbunden.
Wenn man die Bahngeschwindigkeit, die Hülsenabmessungen, die Restlagendicke, die Bahnbreite, die Stoffwerte Elastizitätsmodul und Dichte von Hülse und Papier frei wählt, kann man beliebig viele Resonanzordnungen konstruieren. Früher war zu hören, dass im Tiefdruck Resonanzen bis dritter Ordnung beobachtet worden seien. Diese Aussage muss mit dem jetzigen Wissensstand angezweifelt werden. Mit den Gegebenheiten im Jahre 2007 ist es auszuschließen, dass unter regulären Bedingungen im Rollendruck (Heatset-Rollendruck, Zeitungsdruck, Tiefdruck) Resonzen zweiter oder gar dritter Ordnung auftreten. Allerdings gibt es Situationen, in denen beim Abarbeiten einer Rolle bei einer bestimmten Restlagendicke eine Resonanz ersten Ordnung aufritt und bei einer kleineren Restlagendicke nochmals eine Resonanz erster Ordnung. Dieses vermeintliche Phänomen kann mit der späteren Lambda-Formel II erklärt werden.
6. Die Hülseneinspannung. Der Schwingungsnullpunkt. Die freie Schwingungslänge. Der Pinolenfaktor. Der Einspannfaktor
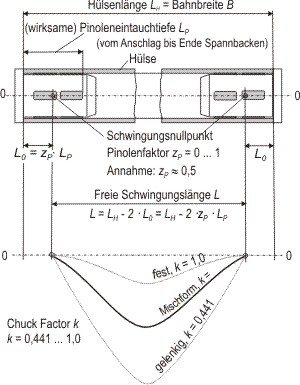
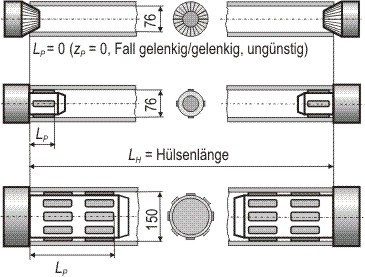
Abbildung 4:: Zur Definition der wirksamen Pinoleintauchtiefe LP, des fiktiven Schwingungsnullpunktes L0 und der freien Schwingungslänge L
Die Lösung der Differenzialgleichung basiert auf folgenden vereinfachenden Annahmen: Der Balken ist als entweder beidseitig fest oder als beidseitig gelenkig anzusehen und die Einspannung selbst habe die Länge null.
Für die antiquierte Koneneinspannung nach Abbildung 4, rechts oben, träfen diese Annahmen zu. Die freie Schwingungslänge wäre identisch mit der Rollenbreite und würde zusammen mit dem Merkmal beidseitig gelenkig zu extrem ungünstig niedrigen Eigenfrequenzen führen. Die Koneneinspannung ist allenfalls noch bei alten oder bei schmalen Rollendruckmaschinen anutreffen.
Bei moderneren Rollenwechslern taucht ein Spanndorn, auch Pinole genannt, mehr oder weniger tief in die Hülse hinein und die Hülse wird in radial nach außen wirkenden Spannbacken gespannt. Bei Rollenwechslern mit Zentrumsantrieb wie z. B. bei Zeitungsdruckmaschinen sind sehr große Spanndrücke aufzubringen, da das gesamte Drehmoment über die Hülse geleitet werden muss. Zusätzlich zur Biegebeanspruchung durch die Schwingungen tritt bei Hülsen für den Zeitungsdruck auch noch eine Torsionsbeanspruchung ein. Große Biegebeanspruchung tritt erst gegen Rollenende auf, große Torsionsbeanspruchung mehr bei der vollen Rolle wie beim Einrichte-Vorrücken oder beim Notstopp.
Durch das Eintauchen der Pinolen in die Hülsen reduziert sich die freie Schwingungslänge der Hülse, die Eigenfrequenz steigt in gewünschter Weise an. Die Pinoleneintauchtiefe kann man nicht in beliebiger Weise steigern, da damit auch die Biegebeanspruchung der Pinole steigt. In dieser Hinsicht wären kurze Pinolen günstiger. Größere Pinoleneintauchtiefen vergrößeren zudem die Baubreite des Rollenwechslers um den doppelten Betrag der größeren Pinoleneintauchtiefe.
Die Abbildung 4 rechts zeigt in der Mitte und unten zeitgemäße Ausführungen von Pinolen: Es existieren Ausführungen mit vier oder acht Spannbacken im Umfang und ein- und zweireihige Ausführungen.
Zur wirksamen Pinoleneintauchtiefe
Für die weitere Behandlung wird die wirksame Pinleneintauchtiefe LP gebraucht. Sie muss mit einer Vereinbarung festgelegt werden. Die Abbildung 4 zeigt rechts den Vorschlag des Autors, der für alle Pinolenkonstruktionen einen eindeutigen Wert liefert.
Zur Lage des Schwingungsnullpunktes
Schwieriger ist die Bestimmung des Schwingungsnullpunktes, in der Abbildung 4 mit L0 bezeichnet. Nach jetzigem und frei verfügbarem Wissensstand ist dieser Schwingungsnullpunkt im physikalischen Sinne weder analytisch berechenbar noch experimentell mit befriedigender Genauigkeit bestimmbar. Für die weitere Behandlung stört dieses Manko nicht, es genügt, bei L0 den fiktiven Nullpunkt anzunehmen, auf den sich die später genannte Korrekturgröße bezieht.
Zum Pinolenfaktor
Leider wird die Annahme des (fiktiven) Schwingungsnullpunktes von den Hülsenherstellern unterschiedlich getroffen. Somit fehlt jede Vergleichsmöglichkeit. Der Autor hat vorgeschlagen, den Schwingungsnullpunkt in der Mitte der wirksamen Pinoleneintauchtiefe anzunehmen. Mit der in der folgenden Formel gezeigten Definition des Pinolenfaktors zP entspräche der Vorschlag des Autors einem zP = 0,5.
| (8) | 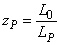 |
Man könnte auch ein anders zP vereinbaren, z. B. zP = 0,75. Die Grenzwerte zP = 0 (Schwingungsnullpunkt ganz außen) und zP = 1 (Schwingungsnullpunkt im inneren Ende der Spannbacken) wären nicht sehr anschaulich und irritierend, aber bei richtiger Handhabe und Deutung möglich. Für zP = 0,5 spricht auch, dass in der Technischen Mechanik bei ähnlichen Problemen auch so verfahren wird. Dass mit zP = 0,5 die Berechnung der freien Schwingungslänge minimal vereinfacht wird, sei nur am Rande erwähnt.
Zur freien Schwingungslänge
Nach den Vorarbeiten kann die für die Berechnung der Eigenfrequenz maßgebende freie Schwingungslänge L der eingespannten Hülse oder Restrolle wie folgt definiert werden:
| (9) | 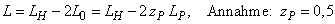 |
Zum Einspannfaktor
Man nimmt zunächst für die Ableitung der Eigenfrequenzformeln an, dass die Hülse beidseitig fest eingespannt ist, wohl wissend, dass diese Annahme in der Praxis nicht zutrifft. Die praktisch erzielbaren Eigenfrequenzen sind wegen der Elastizität der Einspannung immer kleiner als die theoretisch berechneten. Es ist somit notwendig, in die Formeln zur Berechnung der Eigenfrequenz einen empirischen Korrekturfaktor, genauer Einspannfaktor, einzubauen, um Übereinstimmung mit dem praktischen Befund zu erzielen. Wo und wie man das macht, ist im Prinzip gleichgültig, die Korrektur muss nur einheitlich und möglichst zweckmäßig gemacht werden.
Die einfachste Methode besteht sicher darin, die theoretisch berechneten Eigenfrequenzen mit einem Einspannfaktor k zu multiplizieren. Diese Vorgehensweise wird seit langem vom finnischen Hülsenhersteller Ahlstrom (jetzt Sonoco-Alcore) praktiziert. Der Einspannfaktor wurde von Ahlstrom mit Chuck Factor bezeichnet. Aber auch in der früheren Publikation ders Bundesverbandes Druck aus dem Jahre 1988 [2] ist die gleiche Vorgehensweise dokumentiert. Die Autoren schreiben von einem "Erfahrungswert 0,66". Da sie den Schwingungsnullpunkt ganz innen angenommen haben, somit bei zP = 1,0 kann man mit den jetzigen Bezeichnungen auch sagen, der Einspannfaktor betrug bei den damaligen Versuchsdaten (Hülsenlänge bis ca. 3m, Hülseninnendurchmesser 76 mm, ...) k1,0 = 0,66. Dieser Wert erscheint auch aus heutiger Sicht plausibel.
Der Einspannfaktor kann nur empirisch über Frequenzmessungen bestimmt werden. Man misst die Eigenfrequenz der "freien" nackten Hülse in senkrechter Anordnung nach der Hülsennorm DIN ISO 11093-8. Diese Eigenfrequenz sei mit fISO bezeichnet. Dann spannt man die Hülse in den Rollenwechsler ein und misst die Eigenfrequenz fRW. Aus diesen beiden Eigenfrequenzen kann der Einspannfaktor wie folgt ermittelt werden:
| (10) | 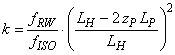 |
Die Formel zeigt, von welchen Größen der Einspannfaktor abhängt. Somit kann man den Einspannfaktor nur für eine gegebene Hülse für einen gegebenen Rollenwechsler korrekt angeben. Die allgemeine Übertragung auf andere Situationen verbietet sich. Ganz schlimm wird die Situation, wenn auf ein und demselben Rollenwechsler die Einspannfaktoren von Hülsen verschiedener Hersteller ermittelt werden und der eine Hülsenhersteller mit zP = 0,5 und der andere mit zP = 0,833 rechnet.
Es ist zwingend notwendig, dass zum Einspannfaktor k auch das verwendete zP angegeben wird, z. B. in einem Index wie folgt: k0,5 für einen Einspannfaktor k ermittelt mit zP = 0,5.7. Die Lambda-Formeln
Erst wenn man die Erkenntnisse und Korrekturen aus dem Kapitel 6 in die Formeln für die Berechnung der Eigenfrequenzen einarbeitet, kommt man zu brauchbaren "Arbeitsformeln". Von der Lösung der Schwingungsdifferenzialgleichung herkommend, hat man es mit Frequenzen zu tun. In der Praxis sind aber Geschwindigkeiten viel anschaulicher. Die Bahngeschwindigkeit ist als Erregergeschwindigkeit konstant, nicht aber die Erregergeschwindigkeit. Die Umstellung der Frequenzformeln auf Geschwindigkeitsformeln ist mit der simplen und allgemeinen Beziehung v = d*π*f in einfachster Weise möglich. An Stelle der ersten Eigenfrequenz oder kritischer Frequenz tritt dann die kritische Geschwindigkeit vkrit.
Die so entstehenden Arbeitsformeln sollen "Lambda-Formeln" genannt werden.
Für die nackte Hülse gilt die Lambda-Formel I:
| (12) | 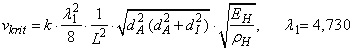 |
Für die Restrolle gilt die Lambda-Formel II:
| (13) | 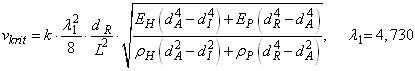 |
Die Zahl "4,730" ist keine magische Zahl, sondern gemäß Tabelle 1 als erste von null verschiedene Lösung der Eigenwertgleichung cos λ * cosh λ - 1 = 0 eindeutig definiert.
Bei Messung nach DIN ISO 11093-8 ist zu setzen: k = 1, L = LH. In allen anderen Fällen ist die freie Schwingungslänge L nach (9) zu berechnen und der Einspannfaktor k einzusetzen.
In beiden Lambda-Formeln steht das L unter dem Bruchstrich im Quadrat. Das bedeutet: Wenn man das L verdoppelt, fällt die kritische Geschwindigkeit auf ein Viertel (!) des ursprünglichen Wertes ab. Damit ist ein Problem nur angedeutet, dass sich bei Breitenzunahmen generell stellt.
In der Lambda-Formel I könnte man die beiden Wurzeln zu einer Wurzel zusammen ziehen. Das ist bewusst nicht gemacht worden. Die erste Wurzel enthält den Geometrie-Term, die zweite den Werkstoffterm. Wenn bei gegebener Papiertbahnbreite die Hülsendurchmesser nicht verändert werden dürfen, dann bleibt nur der Werkstoffterm für eine Erhöhung der kritischen Geschwindigkeit. Man erkennt, dass der E-Modul möglichst hoch und/oder die Dichte möglichst niedrig sein sollte, um hohe kritische Geschwindigkeiten zu erzielen. Das gilt auch für das Restpapier in der Lambda-Formel II. Natürlich wird man das Druckpapier nicht nach diesem Kriterium auswählen. Beim üblichen Hartpapierhülsenwerkstoff sind trotz großer Verbesserungen in den letzten Jahren Grenzen erkennbar. So ist es nicht verwunderlich, dass andere Hülsenwerkstoffe ins Gespräch kommen, wie z. B. Aluminium oder faserverstärkte Kunststoffe. Bei Hartpapier ist die Steigerung des E-Moduls in der Regel mit einem Anstieg der Dichte verbunden. Steigen beide Stoffgrößen um den gleichen relativen Betrag an, hat man in Bezug auf die kritische Geschwindigkeit nichts gewonnen.
Die Lambda-Formel I zeigt, dass nich der E-Modul und auc nicht duie Dichte alleine entscheidend sind. Einzig und alleine ist die Wurzel aus dem Verhältnis von E-Modul zu Dichte proportional zu der kritischen Geschwindigkeit. Wegen dieser Bedeutung wird diese kombinierte Stoffgröße mit spezifische Schwingsteifigkeit SSH bezeichnet.
| (14) | 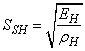 |
Die Schwingsteifigkeit besitzt die Einheit einer Geschwindigkeit, z. B. 2600 m/s. Pysikalisch ist die so definierte Schwingsteifigkeit die Schallgeschwindigkeit in einem Stab aus dem gleichen Werkstoff.
Eingriffe in den Geometrieterm der Lambda-Formel I, z. B. Erhöhung des Innendurchmessers von 150 mm auf 200 mm bringen Verbesserungen der kritischen Geschwindigkeit, die mit Werstoffverbesserungen bei Hartpapierhülsen nie und nimmer erreicht werden können.
In der Diskussion stehen Unterstützungssysteme. Sie sollen die Restrolle in der kritischen Phase im Rollenwechsler unterstützen, d. h. die Schwingungsamplituden begrenzen. Die Diskussion ist nicht neu. Bereits in der BVD-Veröffentlichung aus dem Jahre 1988 [2] wurden neben der Erhöhung der Innendurchmesser vom damaligen Standard 76 mm auf 150 mm auch Unterstützungssysteme angesprochen. Aber sind Unterstützungssysteme nicht auch Krücken für Hülsen, die aus eigener Kraft nicht mehr richtig laufen können?
8. Die Resonanzdurchmesser
Resonanz liegt vor, wenn die Erregerfrequenz fEr nach (7) und Eigenfrequenz fi nach (5.3) bzw. (6.3) übereinstimmen. Man kann auch sagen, wenn die kritische Geschwindigkeit mit der Bahngeschwindigkeit übereinstimmt.Man hat zwei Fälle zu unterscheiden:
- Die E-Moduln und Dichten von Hülse und Papier sind ungefähr gleich und es können die Mittelwerte EM und ρM angegeben werden.
- Der allgemeine Fall. Die Die E-Moduln und Dichten von Hülse und Papier sind verschieden.
8.1 Der spezielle Fall: E-Modul und Dichten von Hülse und Papier ungefähr gleich:
Die Gleichsetzung von (7) mit (5.3) ergibt:
| (15) | 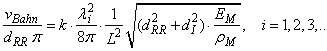 |
Diese Beziehung soll mit "Resonanzbedingung" bezeichnet werden. Aus ihr kann mit einfachen Umformungen der gesuchte Resonanzdurchmesser dRR abgeleitet werden. Nach wenigen Zwischenrechnungen erhält man:
| (16) | 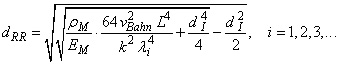 |
Die Formelzeichen:
| ρM | Gemittelte Dichte von Hülse und Papier |
| v = vBahn | Bahngeschwindigkeit |
| L | Freie Schwingungslänge (Hülsenlänge, siehe unten) |
| dI | Hülseninnendurchmesser |
| EM | Gemittelter E-Modul von Hülse und Papier |
| λi | Eigenwerte nach früherer Tabelle entsprechend der Lagerungsart und der Ordnungsnummer. Da es mehrere Eigenwerte gibt (theoretisch unendlich viele), gibt es auch mehrere Resonanzdurchmesser. |
| k | Einspannfaktor (siehe unten) |
Gleiche Werte Stoffwerte für Hülse und Papier kann man allenfalls für ganz einfache Hülsenqualitäten in Verbindung mit Zeitungspapier annehmen. Somit sind der praktischen Anwendung der Formel (XXXX???) sehr enge Grenzen gesetzt. Dennoch ist die Formel für Demo- und Ausbildungszwecke wertvoll, da sie die wesentlichen Zusammenhänge klar erkennen lässt und das Verständnis fördert. Für die letztgenannten Zwecke sollte man zur weiteren Vereinfachung den Einspannfaktor k auf 1 setzen und die freie Schwingungslänge L gleich der Hülsenlänge LH. Nur zur Veranschaulichung soll das folgende Beispiel mit völlig absurden Daten dienen:
EM = 2000 N/mm2 = 2000*106 N/m2
ρM = 900 kg/m3
L = 2,5 m
vBahn = 16 m/s
dI = 76 mm = 0,076 m
Statt mit dem Einspannfaktor soll gleich mit dem "worst case", d. h. mit den ungünstigen Fall
der beidseitig gelenkigen Einspannung gerechnet werden,
also mit λi = i * π.
Diese Daten führen zu folgenden Resonanzdurchmessern:
| Resonanz- ordnung |
Resonanz- durchmesser |
| i = 1 | 227,0 mm |
| i = 2 | 104,9 mm |
| i = 3 | 61,7 mm |
Man kann bei diesem absurden Beispiel erkennen, dass Resonanzen rechnerisch nur bis zur Ordnung 1 auftreten können, wenn man den Hülsenaussendurchmesser mit 106 mm annimmt. Aber dieser Wert liegt noch ziemlich nahe an der Resonanz zweiter Ordnung. Bei der Resonanz dritter Ordnung wäre der Resonanzdurchmesser schon kleiner als der Hülseninnendurchmesser, somit scheidet diese Resonanzordnung und alle höheren aus. Wie schon ausgeführt, sind unter realistischen Bedingungen im Rollendruck Resonanzen höherer Ordnung als 1 nicht zu erwarten.
8.2 Der allgemeine Fall: E-Moduln und Dichten von Hülse und Papier verschieden
Die Gleichsetzung von (7) mit (6.3) führt zur Resonanzbedingung:
| (17) | 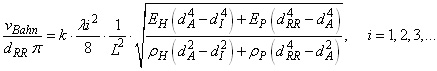 |
9. Das Programm Papierrollenschwingungen
Die Funktionalität des Programms geht über die Berechnung der Eigenfrequenz oder der kritischen Geschwindigkeit hinaus. Die folgenden Hardcopies sollen einen Eindruck vermitteln.
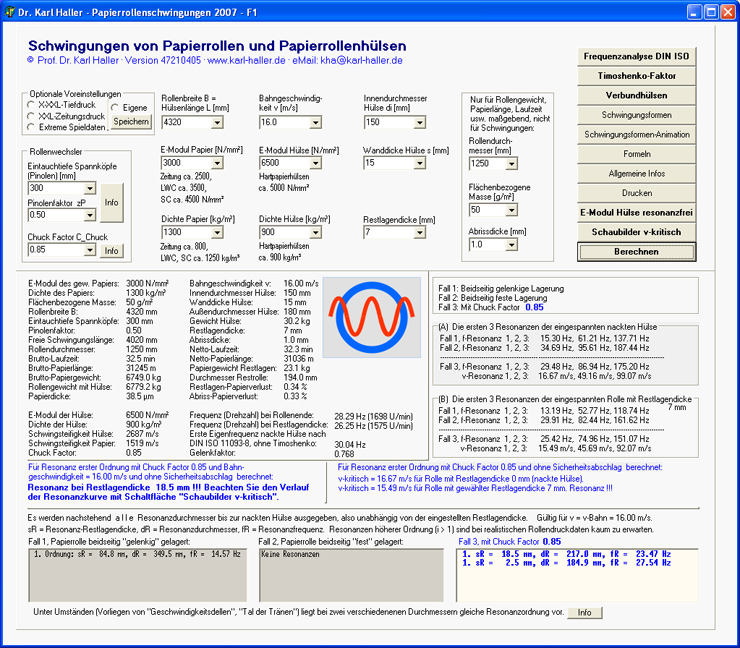
Abbildung 5: Das Hauptmenü
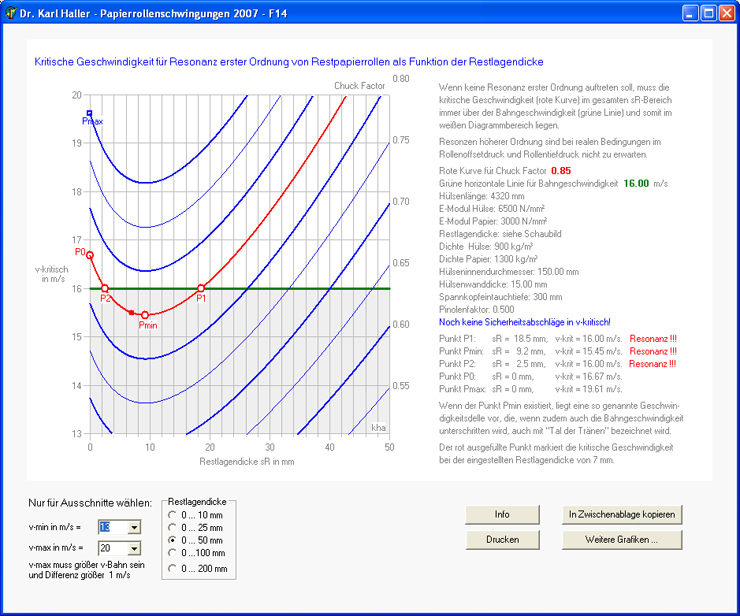
Abbildung 6: Kritische Geschwindigkeit in Anhängigkeit von der Restlagendicke
-->
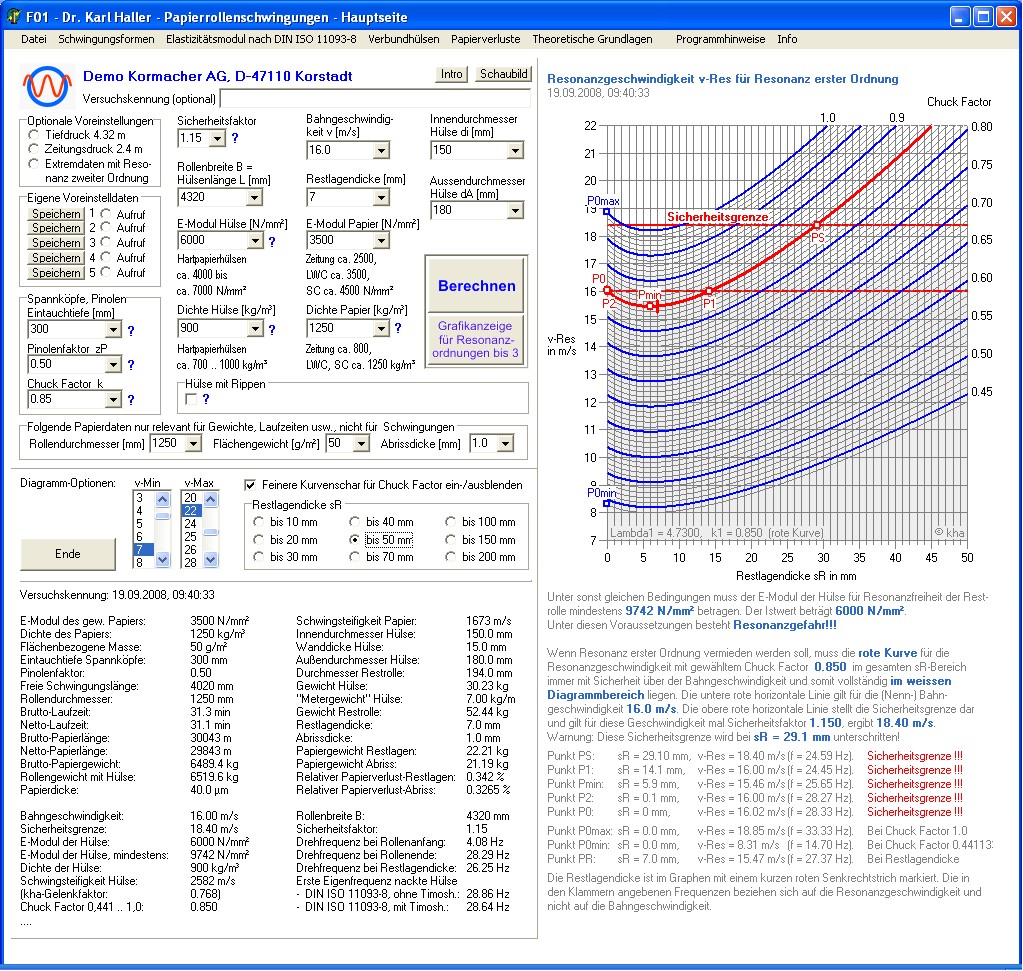
Abbildung 5: Das Hauptmenü des Programms Papierrollenschwingungen
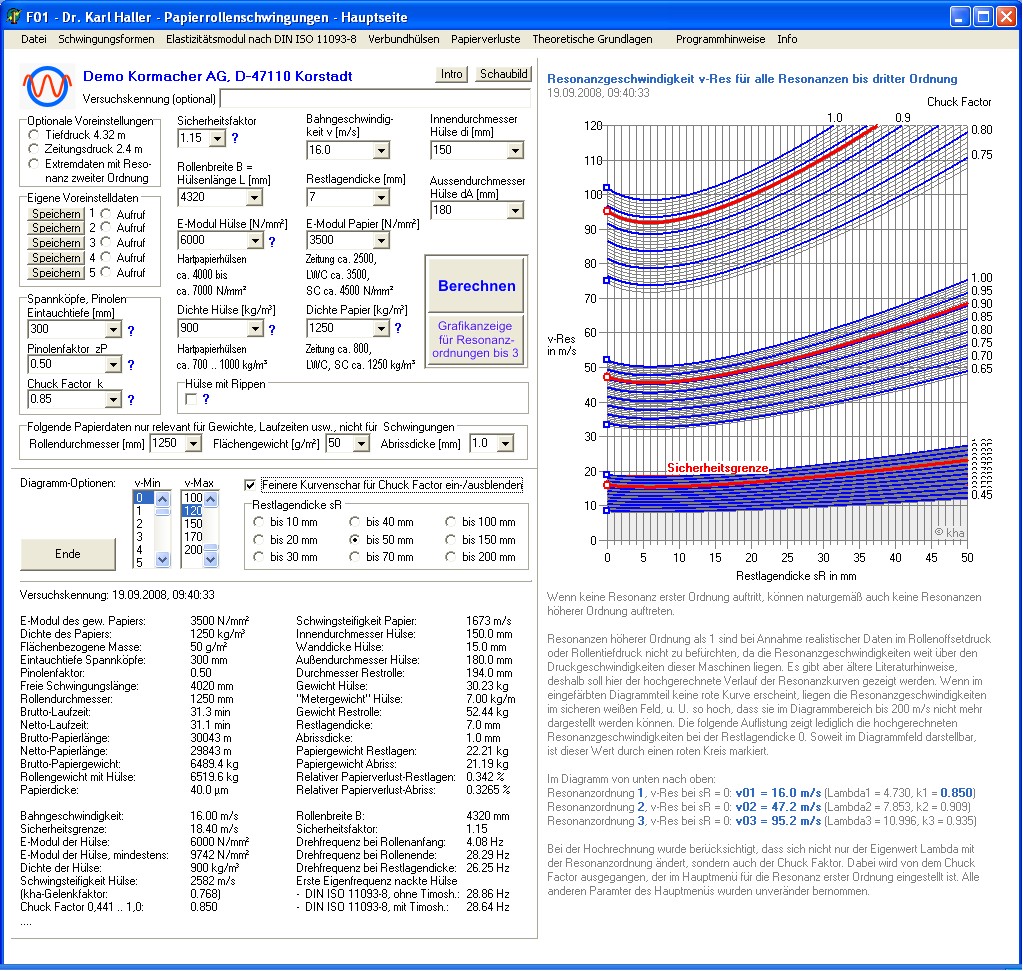
Abbildung 6: Hauptmenü mit Anzeige aller Resonanzkurven bis zur Ordnung drei
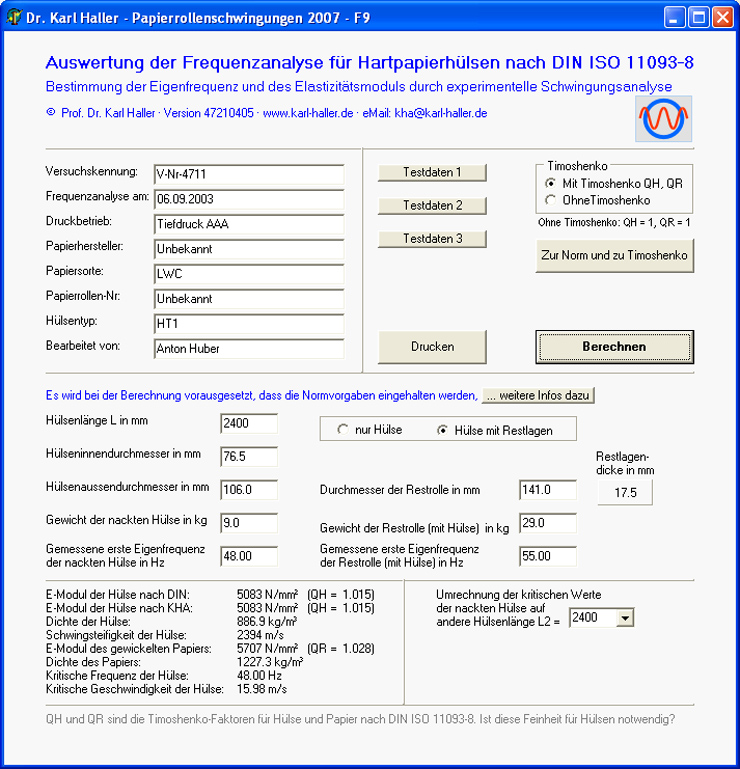
Abbildung 7: Frequenzanalyse
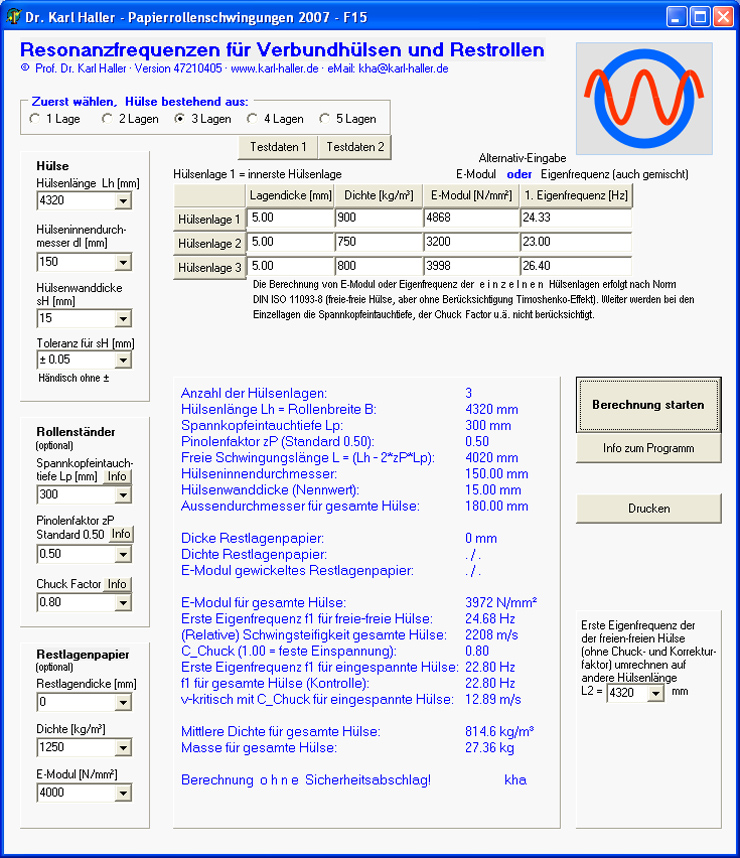
Abbildung 8: Verbundhülsen
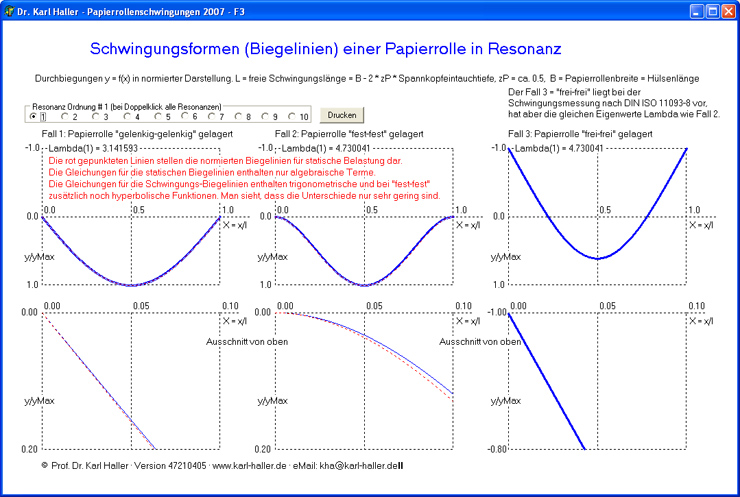
Abbildung 9: Schwingungsformen
10. Geschwindigkeitsdellen
Man sollte annehmen, dass die kritische Geschwindigkeit mit abnehmender Restlagendicke monoton abfällt. Für die meisten Hülsen-/Papierkombinationen im Feld der 76er Hülsen trifft dieses auch zu. Bei den meisten Hülsen-/Papierkombinationen im Feld der 150er Hülsen ist ein monotoner Kurvenverlauf eher die Ausnahme. Meistens zeigt sich die Ausprägung eines ausgesprochenen Minimums, wie die Abbildung 6 zeigt. Diese Erscheinung ist kein Phänomen sondern erklärt sich aus der Lambda-Formel II. Die Erscheinung eines "Minimums" in der Darstellung mit der kritischen Geschwindigkeit soll mit "Geschwindigkeitsdelle" bezeichnet werden. Die genauen mathematischen Zusammenhänge sind zwischenzeitlich geklärt. Es kann genau angegeben werden, unter welchen Bedingungen "Geschwindigkeitsdellen" auftreten. Im gezeigten Programm ist auch ein Rechenmodul enthalten, mit dem das Minimum der Geschwindigkeitsdelle (in Abbildung 6 der Punkt Pmin) exakt berechnet werden kann, also die minimale kritische Geschwindigkeit und die zugehörige Restlagendicke.
Natürlich ist es wünschenswert, dass die Hülsen bzw. die Restrollen dieses Minimum mit ausreichendem Sicherheitsabstand durchstehen.
11. Das Programm Papierrollenschwingungen-LT
Für einfache Anwendungen wird der große Leistungsumfang des Programms "Papierrollenschwingungen" nicht benötigt und deshalb hat der Verfasser eine einfache Lösung (Light-Version) in Form einer Excel-Datei erstellt.Nach eigener Vorgabe sollte die Excel-Datei keine Makros enthalten, damit beim Download von Virenschutzporgrammen keine störenden Warnmeldungen produziert werden. Durch den Verzicht auf Makros können aber keine Plausiblitätskontrollen der Eingabedaten durchgeführt werden. Der Benutzer ist für die richtige Eingabe die Daten selbst verantwortlich. Fixe Kontrolldaten sollen Entgleisungen verhindern.
Mit Ausnahme der gelb markierten Eingabefelder sind die anderen Zellen schreibgeschützt, so dass z. B. kein versehentliches Ändern der Berechnungsformel möglich ist. Die Bedienung ist ansonsten selbsterklärend.
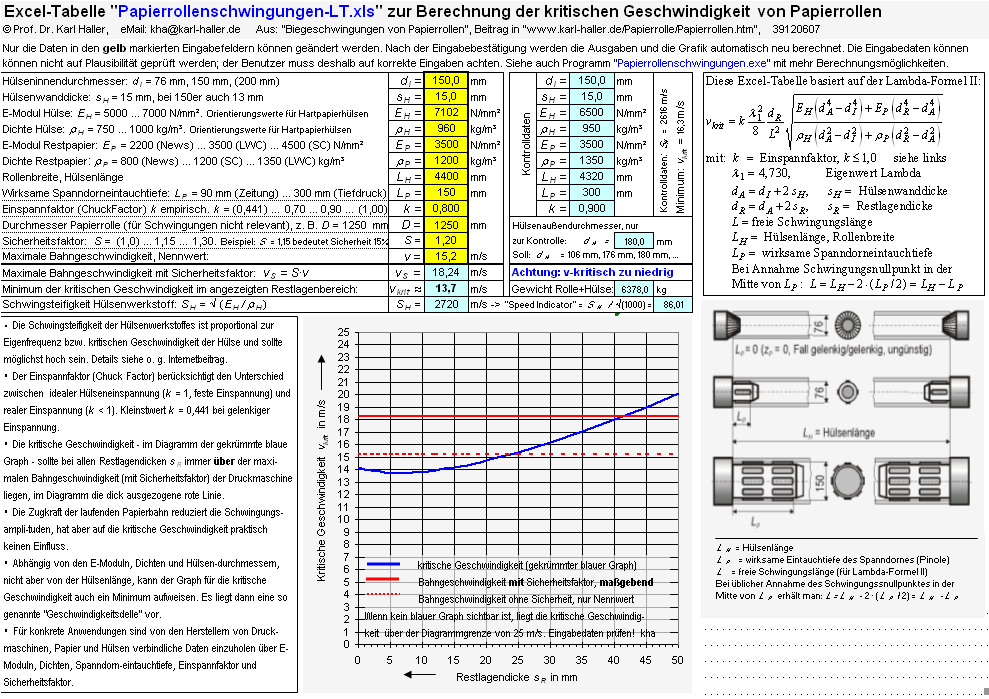
Abbildung 10: Die Light-Version des Programms zur Berechnung der Papierrollenschwingungen
12. Zusammenfassung
In dieser Abhandlung wurde das Schwingungsverhalten von Papierrollen mathematisch untersucht. Das Thema ist besonders bei breiten und schnellen Tiefdruckmaschinen und auch für 6-Seiten-breite Zeitungsdruckmaschinen relevant und wird in Zukunft noch bedeutender.
13. Literaturhinweise
| [1] | Dr.-Ing. Willy Heckers, "Beanspruchungen von Rollenhülsen beim Wickeln", Vortrag bei der Jahrestagung 1982 des Vereins Deutscher Druckingenieure (VDD) |
| [2] | Dr.-Ing. Manfred König, Dipl.-Ing. Dirk Müller, "Hartpapierhülsen in Papierrollen im Tiefdruck". Technischer Informationsdienst des Bundesverbandes Druck e.V., Wiesbaden, 1988. Nachtrag August 2004: PDF-Version des genannten Informationsdienstes, ca. 650 KB. Die Veröffentlichung erfolgt mit freundlicher Genehmigung des Bundesverbandes Druck und Medien (BVDM) e.V., Wiesbaden, August 2004. Dateigröße ca. 612 KB. Siehe auch [5]. |
| [3] | Niko Ruokosuo, "Newspaper reel core and chuck specification", IFRA Special Report 1.8, Darmstadt, 1993 |
| [4] | N.N, "Druckleistung auf höchstem Niveau – Breiten- und Geschwindigkeitsentwicklung im Publikationstiefdruck", KBA Report No. 12, 1/1999, Koenig & Bauer AG, Würzburg |
| [5] | Prof. Dr.-Ing. Karl Haller, "Hülsen für Papierrollen im Tiefdruck", bvdm-Expertenpapier, 7/2007, Bundesverband Druck und Medien bvdm e.V., Wiesbaden, Art.-Br. 85601. Mit freundlicher Genehmigung des bvdm wird eine PDF-Version des Expertenpapiers zum Download angeboten. Dateigröße ca. 2,9 MB. |
| [6] | Prof. Dr.-Ing. Karl Haller, "Schwingungen von Papierrollen in Druckmaschinen", Beitrag zum Jahrbuch 2008 des Vereins Deutscher Druckingenieure VDD, 9/2008. |
Stand: 27.11.1999 / 31.05.2008, Dr. K. Haller